УРАВНЕНИЕ ШРЕДИНГЕРА
И ЕГО ЧАСТНЫЕ СЛУЧАИ (продолжение): прохождение частицы через ПОТЕНЦИАЛЬНЫЙ БАРЬЕР, Гармонический осциллятор

Прохождение частицы через потенциальный барьер для классического случая нами уже рассматривался в ЛЕКЦИИ 7 ЧАСТИ 1 (см. рис. 7.2). Рассмотрим теперь микрочастицу, полная энергия которой меньше уровня U потенциального барьера (рис. 19.1). В классическом варианте в этом случае прохождение частицы через барьер невозможно. Однако в квантовой физике существует вероятность, что частица пройдет. Причем она не "перепрыгнет" через него, а как бы "просочится", употребив свои волновые качества. Поэтому эффект еще называется "туннельным". Для каждой из областей I, II, III запишем стационарное уравнение Шредингера (18.3).

Для I и III : , (19.1, а)

для II: https://pandia.ru/text/78/010/images/image005_107.gif" width="71" height="32">, где a = const. Тогда и y" = . Подстановка y" в (19.1a) дает: Искомое общее решение для области I запишется в виде суперпозиции

https://pandia.ru/text/78/010/images/image010_62.gif" width="132" height="32 src="> . (19.3)

В этом случае начальная точка распространения волны сдвинута на L , a В 3 = 0 , поскольку в области III имеется только проходящая волна.

В области II (барьер) подстановка y" в (19.1б) дает

https://pandia.ru/text/78/010/images/image012_51.gif" width="177" height="32">.

Вероятность прохождения характеризуется коэффициентом прохождения - отношением интенсивности прошедшей волны к интенсивности падающей:

(0) = y2"(0) , y2"(L ) = y3"(L ); (19.5)

из которых первые два означают "сшивание" функций на левой и на правой границах барьера, а третье и четвертое - гладкость такого перехода. Подставляя в (19.5) функции y1, y2 и y3, получим уравнения

Поделим их на А 1 и обозначим a 2=A 2/A 1; b 1=B 1/A 1; a 3=A 3/A 1; b 2=B 2/A 1.

. (19.6)

Умножим первое уравнение (19.6) на i k и сложим со вторым. Получим 2 i k = a 2(q + i k ) - b 2(q - i k ) . (19.7)

Вторую пару уравнений (19.6) будем рассматривать как систему двух уравнений с неизвестными a 2 и b 2.

Детерминанты этой системы:

https://pandia.ru/text/78/010/images/image017_33.gif" width="319" height="32">,

где e-qL (q+ i k) 2 » 0, т. к. qL >> 1.

Поэтому https://pandia.ru/text/78/010/images/image019_32.gif" width="189" height="63">, и, чтобы найти модуль комплексной величины а 3, умножим числитель и знаменатель полученной дроби на (q + i k )2. После простых преобразований получим

https://pandia.ru/text/78/010/images/image021_30.gif" width="627" height="135 src=">Обычно E/U ~ 90% и весь коэффициент перед "е" имеет порядок единицы. Поэтому вероятность прохождения частицы через барьер определяется следуюшим соотношением:

https://pandia.ru/text/78/010/images/image023_24.gif" width="91" height="44">.

Это означает, что при E < U частица барьера не преодолеет, т. е. туннельный эффект в классической физике отсутствует.

Этот эффект используется в инженерной практике для создания туннельных диодов, широко применяемых в радиотехнических устройствах (см. ЧАСТЬ 3, ЛЕКЦИЯ 3).

Кроме того, оказалось возможным инициировать в земных условиях термоядерную реакцию синтеза, которая на Солнце идет в обычных для Солнца условиях - при температуре T ~ 109 K . На Земле такой температуры нет, однако, благодаря туннельному эффекту, есть вероятность запуска реакции при температуре T ~ 107 K , имеющей место при взрыве атомной бомбы, которая и явилась запальным устройством для водородной . Более подробно об этом в следующей части курса.

Гармонический осциллятор. Классический гармонический осциллятор нами также уже рассматривался (ЛЕКЦИИ 1,2 ЧАСТИ 3). Им, например, является пружинный маятник, полная энергия которого E = mV 2/2 + kx 2/2. Теоретически эта энергия может принимать непрерывный ряд значений, начиная от нуля.

Квантовый гармонический осциллятор - это колеблющаяся по гармоническому закону микрочастица, находящаяся в связанном состоянии внутри атома или ядра. При этом потенциальная энергия остается классической, характеризуя аналогичную упругую возвращающую силу kx . Учитывая, что циклическая частота получим для потенциальной энергии https://pandia.ru/text/78/010/images/image026_19.gif" width="235" height="59">. (19.9)

В математическом отношении задача эта еще более сложная, чем предыдущие. Поэтому ограничимся констатацией того, что получится в результате. Как и в случае с одномерной ямой, мы получим дискретный спектр собственных функций и собственных энергий, и одному собственному значению энергии будет соответствовать одна волновая функция: En Û yn (нет вырождения состояний, как в случае с трехмерной ямой). Плотность вероятности |yn|2 также представляет собой осциллирующую функцию, однако высота "горбов" различна. Это уже не банальный sin 2 , а более экзотические полиномы Эрмита Hn (x ). Волновая функция имеет вид

, где С n - зависящая от n константа. Спектр собственных значений энергий:

, (19.10)

где квантовое число n = 0, 1, 2, 3 ... . Таким образом, существует и "нулевая энергия" , выше которой спектр энергий образует "этажерку", где полочки расположены на одинаковом расстоянии друг от друга (рис. 19.2). На том же рисунке для каждого уровня энергии показана соответствующая плотность вероятности |yn|2, а также потенциальная энергия внешнего поля (пунктирная парабола).

Существование отличной от нуля минимально возможной энергии осциллятора имеет глубокий смысл. Это означает, что колебания микрочастиц не прекращаются никогда , что в свою очередь означает недостижимость абсолютного нуля температуры.

1. , Бурсиан физика: Курс лекций с компьютерной поддержкой: Учеб. пособие для студ. высш. учеб. заведений: В 2 т. – М.: Изд-во ВЛАДОС-ПРЕСС, 2001.

В принципе ничего особенного, их можно найти в таблицах и даже построить графики.

Пусть частица движется вдоль оси X. При этом движение ограничено отрезком (0,l ). В точках x=0 и x=l установлены непроницаемые бесконечно высокие стенки. Потенциальная энергия в этом случае имеет вид

Такая зависимость потенциальной энергии от x получила название потенциальной ямы .

Запишем стационарное уравнение Шредингера

Поскольку пси-функция зависит только от координаты x, то уравнение упрощается следующим образом

Внутри потенциальной ямы U=0

За пределы потенциальной ямы частица попасть не может. Поэтому вероятность обнаружения частицы вне ямы равна нулю. Соответственно и пси-функция за пределами ямы равна нулю. Из условия непрерывности следует, что ψ должна быть равна нулю и на границах ямы, т.е. . Это граничное условие, которому должны удовлетворять решения уравнения.

Введем обозначение

и получим уравнение, хорошо известное из теории колебаний

Решение такого уравнения имеет вид гармонической функции

Выбор соответствующих параметров k и α определяется граничными условиями, а именно,

n = 0 отпадает, т.к. в этом случае ψ = 0 и частица нигде не находится. Следовательно, число k принимает лишь определенные дискретные значения, удовлетворяющие условию . Отсюда следует очень важный результат. Найдем собственные значения энергии частиц

т.е. энергия электрона в потенциальной яме не произвольна, а принимает дискретные значения, т.е. является квантованной. Величина Е n зависит от целого числа n , которое принимает значение от 1 до ∞ и носит название главного квантового числа . Квантованные значения энергии называются энергетическими уровнями, а квантовое число n определяет номер энергетического уровня . Таким образом, электрон в потенциальной яме может находиться на определенном энергетическом уровне E n . Причем минимальное значение энергии, соответствующее первому энергетическому уровню, отлично от нуля

.

Определим расстояние между соседними энергетическими уровнями

При больших m и l расстояние между уровнями становится мало, и спектр становится квазинепрерывным. Относительное расстояние между уровнями

при n → ∞ ,

т. е. спектр становится непрерывен. В этом заключается принцип соответствия Бора : при больших квантовых числах выводы и результаты квантовой механики должны соответствовать классическим результатам.

Вернемся к задаче определения собственных функций. После применения граничных условий имеем

Для нахождения коэффициента А воспользуемся условием нормировки

Значение интеграла равно l /2.

Таким образом, собственные функции имеют вид

Графики собственных функций имеют вид

Окончательно сформулируем основные выводы :

1. Энергетический спектр частицы в потенциальной яме дискретный – энергия квантуется.

2. Минимальное значение кинетической энергии не может быть равно нулю.

3. Дискретный характер энергетических уровней проявляется при малых m , l и n , при больших m , l ,n движение становится классическим.

4. Положения микрочастицы в яме не равновероятны, а определяются собственными функциями, в то время как в случае классической частицы все положения равновероятны.

Вопросы для самоконтроля:

1. Как определить вероятность нахождения частицы в некоторой точке?

2. Что называется потенциальной ямой?

3. Каково значение уравнения Шредингера? Что позволяет найти уравнение Шредингера?

4. Какие условия накладываются на пси-функцию?

5. Каков физический смысл главного квантового числа?

6. Почему квантовая механика является статистической теорией?

7. В чем состоит принцип соответствия Бора?

Временное и стационарное уравнение Шредингера

Статистическое толкование волн де Бройля и соотношение неопределенностей Гейзенберга привели к выводу, что уравнением движения в квантовой механике, описывающим движение микрочастиц в различных силовых полях, должно быть уравнение, из которого бы вытекали наблюдаемые на опыте волновые свойства частиц. Основное уравнение должно быть уравнением относительно волновой функции (x,y,z,t), так как именно она, или точнее, величина 2 , определяет вероятность пребывания частицы в момент времени t в объеме dV, т.е. в области с координатами х и х+dx, y и y+dy, z и z+dz. Так как искомое уравнение должно учитывать волновые свойства частиц, то оно должно быть волновым уравнением, подобно уравнению, описывающему электромагнитные волны.

Это уравнение постулируется, а его правильность подтверждается согласием с опытом получаемых с его помощью результатов.

Основное уравнение нерелятивистской квантовой механики (1926 г.)

4.1.Временное уравнение Шредингера:

Уравнение справедливо для нерелятивистских частиц << ,

где {\displaystyle \hbar ={h \over 2\pi }} – масса частицы; - мнимая единица; – потенциальная функция частицы в силовом поле, в котором она движется; – искомая волновая функция; ∆ – оператор Лапласа

Условия, накладываемые на волновую функцию:

Волновая функция должна быть конечной, однозначной и непрерывной.

Производные ∂Ψ/∂x, ∂Ψ/∂y, ∂Ψ/∂z , ∂Ψ/∂t должны быть непрерывны.

Функция 2 должна быть интегрируема (это условие сводится к условию нормировки вероятностей).

4.2.Стационарное уравнение Шредингера

В случае стационарного силового поля (функция U=U(x, у, z) не зависит явно от времени и имеет смысл потенциальной энергии. В данном случае решение уравнения Шредингера может быть представлено в виде произведения двух функций, одна из которых есть функция только координат, другая - только времени, причем зависимость от времени выражается множителем ).

Тогда волновая функция для стационарных состояний (состояний с фиксированными значениями энергии) может быть представлена в виде:

Стационарное уравнение Шредингера:

получилось после подстановки волновой функции во временное уравнение Шредингера и преобразований (∆ - оператор Лапласа, m – масса частицы; - приведенная постоянная Планка ( = h/2π ); E – полная энергия частицы, U – потенциальная энергия частицы. В классической физике величина (E –U )равнялась бы кинетической энергии частицы. В квантовой механике вследствие соотношения неопределенностей понятие кинетической энергии лишено смысла. Здесь потенциальная энергия U – это характеристика внешнего силового поля , в котором движется частица. Это величина вполне определенная. Она также является функцией координат, в данном случае U =U (x,y,z)).

где – оператор Гамильтона – аналог классической функции Гамильтона

в которой и заменены операторами импульса x , y , z и координаты , , :

х → = х, y → = y, z → = z,

(4.2)

Уравнение Шредингера Зависящее от времени уравнение Шредингера: где – гамильтониан системы. Разделение переменных. Запишем Ψ(,t) = ψ()θ(t), где ψ является функцией координат, а θ – функция времени. Если не зависит от времени, тогда уравнение ψ = iћψ принимает вид θψ = iћψθ или Левая часть является функцией только координат, а правая не зависит от переменной x. Поэтому обе части последнего уравнения должны быть равны одной и той же постоянной, которую обозначим E Следовательно, θ(t) = exp(−iEt/ћ), ψ() = Eψ() и Ψ(,t) = ψ()exp(−iEt/ћ). Уравнение ψ() = Eψ() называют стационарным уравнением Шредингера. Для одномерной системы с массой m в поле с потенциалом U(x) оно принимает вид: или Для трехмерной системы с массой m в поле с потенциалом U(): −(ћ 2 /2m)Δψ() + U()ψ() = Eψ(), где Δ – лапласиан.

Так как уравнение Шредингера является линейным уравнением первого порядка по времени, то с его помощью по заданному значению волновой функции Ψ(x, y, z, 0) в момент времени t = 0 можно найти её значение в произвольный момент времени t − Ψ(x, y, z, t).

Уравнение Шредингера для стационарного состояния, когда потенциальная энергия частицы не зависит от времени, имеет вид

ψ() = Eψ().

(4.3)

Это уравнение называют стационарным уравнением Шредингера.

Так как в стационарном состоянии

Ψ(,t) = ψ()exp(−iEt/ћ)

(4.4)

и вероятность найти частицу в момент t в точке x, y, z пропорциональна |Ψ(,t)|, то она ~ |ψ(x,y,z)| 2 , т.е. не зависит от времени. Аналогично, вероятность обнаружить значение физической величины, характеризующей систему, также не изменяется со временем, поскольку выражается через квадрат модуля волновой функции.

4.2 . Частица в одномерной прямоугольной яме с бесконечными стенками

Потенциальная энергия U(x) в прямоугольной яме удовлетворяет следующим условиям:

Частица находится в области 0 ≤ x ≤ L. Вне этой области ψ(x) = 0. Уравнение Шредингера для частицы, находящейся в области 0 ≤ x ≤ L

где k = (2mE/ћ 2) 1/2 . Из граничных условий ψ(0) = 0, ψ(L) = 0 и условий непрерывности волновой функции следует

Частица может находиться в каком-то одном из множества дискретных состояний, доступных для неё.
Каждому значению энергии E n соответствует волновая функция ψ n (x), которая с учетом условия нормировки

имеет вид

(4.10)

В отличие от классической, квантовая частица в прямоугольной яме не может иметь энергию
E < ћ 2 π 2 /(2mL 2). Состояния частицы ψ n в одномерном поле бесконечной потенциальной ямы полнос­тью описывается с помощью одного квантового числа n. Спектр энергий дискретный.

Рис. 4.2. Уровни энергии и волновые функции частицы Ψ в бесконечной прямоугольной яме. Квадрат модуля волновой функции |Ψ| 2 определяет вероятность нахождения частицы в различных точках потенциальной ямы.

4.3 . Гармонический осциллятор

Положение уровней частицы в потенциальной яме зависит от вида потенциальной ямы. В одномерной потенциальной яме гармонического осциллятора потенциальная энергия имеет вид

Допустимые значения полной энергии определяются формулой

E n = ћω 0 (n + 1/2), n = 0, 1, 2,

(4.13)

В отличие от бесконечной прямоугольной ямы, спектр уровней гармонического осциллятора эквидистантный.
С увеличением массы частицы или размеров области ее локализации квантовое описание частицы переходит в классическое.

4.4 . Частица в поле с центральной симметрией

В сферических координатах стационарное уравнение Шредингера для частицы в центральном потенциале U(r) имеет вид

где радиальная функция R nl (r) и угловая функция Y lm (θ,φ), называемая сферической, удовлетворяют уравнениям

2 Y lm (θ,φ) = ћ 2 l (l +1)Y lm (θ,φ)

(4.16)

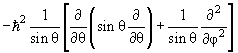Y lm (θ,φ) = ћ 2 l (l +1)Y lm (θ,φ)

(4.17)

Уравнение (4.16) определяет возможные собственные значения l и собственные функции Y lm (θ,φ) оператора квадрата момента 2 . Уравнение (4.17) определяет собственные значения энергии Е и радиальные собственные функции R nl (r), от которых зависит энергия системы (рис. 4.3).
Схема уровней (последовательность и абсолютные значения энергий) зависит от радиальной функции R nl (r), которая в свою очередь определяется потенциалом U(r), в котором находится частица.

Рис. 4.3. Радиальное распределение вероятности нахождения электрона в кулоновском поле протона (атом водорода). Расстояния даны в боровских радиусах
r 0 = ћ 2 /m e e 2 ≈ 0.529·10 8 cм.

4.5 . Орбитальный момент количества движения

Собственные значения L 2 и L z являются решением уравнений

2 Y lm (θ,φ) = L 2 Y lm (θ,φ) и z Y lm (θ,φ) = L z Y lm (θ,φ).

Они имеют следующие дискретные значения

L 2 = ћ 2 l(l + 1), где l = 0, 1, 2, 3, …,
L z = ћm, где m = 0, ± 1, ± 2, ± 3,…, ± l.

Для характеристики состояний с различными значениями орбитального момента l обычно используют следующие обозначения:

Спектроскопические названия орбитальных моментов l

l = 0	s-состояние
l = 1	p-состояние
l = 2	d-состояние
l = 3	f-состояние
l = 4	g-состояние
l = 5	h-состояние
и. т. д.

Состоянию с l = 0 отвечает сферически симметричная волновая функция. В тех случаях, когда l ≠ 0 волновая функция не имеет сферической симметрии. Симметрия волновой функции определяется симметрией сферических функций Y lm (θ,φ). Имеет место интересное квантовое явление, когда решение сферически симметричной задачи (потенциал описывает сферически симметричную систему) приводит к состояниям, не обладающим сферической симметрией. Таким образом, симметрия уравнений не обязательно должна отражаться в симметрии каждого отдельно взятого решения этих уравнений, а лишь во всей совокупности этих решений.
Для частицы, находящейся в сферически симметричном потенциале, величина орбитального момента количества движения L:

(4.18)

Обычно, для упрощения, когда говорят о величине орбитального момента количества движения, называют этой величиной квантовое число l, имея в виду, что между l и L имеется однозначная связь (4.18).

Так как величина l может принимать только целочисленные значения 0, 1, 2, 3,…, то и орбитальный момент количества движения L квантуется. Например, для частицы с l = 2 момент количества движения

=
= 6.58·10 -22 √6 МэВ·сек ≈ 2.6·10 - 34 Дж·сек.

Пространственное квантование . Орбитальный момент количества движения является векторной величиной. Так как величина орбитального момента количества движения квантуется, то и направление по отношению к выделенному направлению z, например, к внешнему магнитному полю, также квантуется и принимает дискретные значения Lz = ћm, где m изменяется от +l до –l, т. е. имеет 2l + 1 значений. Например, при l = 2 величина m принимает значения +2, +1, 0, -1, -2 (см. рис. 4.4). Вместе с тем энергия системы не зависит от m, т. е. от направления вектора , что является очевидным следствием сферической симметрии системы.
Состояние частицы, находящейся в сферически симметричном поле, полностью описывается тремя квантовыми числами: n, l и m.
Появление квантовых чисел связано со свойствами симметрии системы. Характер этой симметрии определяет возможные значения квантовых чисел. Очевидно, что система, описываемая функцией e im φ , примет прежнее значение только тогда, когда азимутальный угол φ в результате поворота вокруг оси z примет прежнее значение φ. Этому условию функция e im φ удовлетворяет только в случае, когда величина mφ кратна 2π. Т.е. величина m должна иметь целые значения. Так как необходимо учитывать вращение в двух противоположных направлениях и отсутствие вращения, единственно возможными значениями оказываются m = 0, ±1, ±2, … .

4.6 . Спин

Спин − собственный момент количества движения частицы. Между значением вектора спина и квантовым числом спина s выполняется такое же соотношение, как между величиной значением вектора орбитального момента и орбитальным квантовым числом l:

2 = ћ 2 s(s + 1)

(4.19)

В отличие от орбитального квантового числа l, которое может быть лишь целым числом или нулем, спиновое квантовое число s (в дальнейшем просто спин) может быть как целым (включая нуль), так и полуцелым, т. е. s = 0, 1/2, 1, 3/2, 2, 5/2, … , но при этом для каждой элементарной частицы спин может принимать единственное присущее этому типу частиц значение . Так, спины π-мезонов и К-мезонов равны 0. Спины электрона, протона, нейтрино, кварков и их античастиц равны 1/2. Спин фотона равен 1. Бозоны составляют класс частиц с целым значением спина, спин фермионов имеет полуцелое значение. Спин частицы невозможно изменить, также как её заряд или массу. Это её неизменная квантовая характеристика.
Как и в случае других квантовых векторов, проекция вектора спина на любое фиксированное направление в пространстве (например, на ось z) может принимать 2s + 1 значение:

s z ћ = ±sћ, ±(s − 1)ћ, ±(s − 2)ћ,..., ±1/2ћ или 0.

Число s z − это квантовое число проекции спина. Максимальная величина s z совпадает с s. Так как спин электрона равен 1/2, то проекция этого спина может принимать лишь два значения s z = ±1/2. Если проекция +1/2, то говорят, что спин направлен вверх, если проекция -1/2, то говорят, что спин направлен вниз.

4.7 . Полный момент количества движения

Полный момент количества движения частицы или системы частиц является векторной суммой орбитального и спинового моментов количества движения.

Квадрат полного момента имеет значение:

2 = ћ 2 j(j + 1).

Квантовое число полного момента j, соответствующее сумме двух векторов и , может принимать ряд дискретных значений, отличающихся на 1:

j = l + s, l + s −1,..., |l − s|

Проекция на выделенную ось J z также принимает дискретные значения:

J z = ћj z ; = -j, -j + 1,..., j − 1, j.

Число значений проекции J z равно 2j + 1. Если для и определены единственные значения проекций на ось z l z и s z , то j z также определена однозначно: j z = l z + s z .

4.8 . Квантовые числа

Квантовые числа – это целые или дробные числа, которые определяют все возможные значения физической величины, характеризующей различные квантовые системы – атомы, атомные ядра, кварки и другие частицы.

Таблица квантовых чисел

n	Радиальное квантовое число. Определяет число узлов волновой функции и энергию системы. n = 1, 2, …, ∞.
J, j	Полный угловой момент J и его квантовое число j. Последнее никогда не бывает отрицательным и может быть целым или полуцелым в зависимости от свойств рассматриваемой системы. 2 = ћ 2 j(j + 1).
L, l	Орбитальный угловой момент L и его квантовое число l. Интерпретация l такая же, как j, но l может принимать только целые значения, включая нуль: l = 0, 1, 2,…. L 2 = ћ 2 l(l + 1).
m	Магнитное квантовое число. Проекция полного или орбитального углового момента на выделенную ось (обычно ось z) равна mћ. Для полного момента m = ±j, ±(j-1), …, ±1/2 или 0. Для орбитального m = ± l, ± (l-1), …, ±1, 0.
S, s	Спиновый угловой момент S и его квантовое число s. Оно может быть либо положительным целым (включая нуль), либо полуцелым. s – неизменная характеристика частицы опреде­лен­ного типа. S 2 = ћ 2 s(s + 1).
s z	Квантовое число проекции спинового момента частицы на выделенную ось. Эта проекция может принимать значения s z ћ, где s z = ± s, ± (s -1), …, ±1/2 или 0.
P или π	Пространственная четность. Характеризует поведение системы при пространственной инверсии → - (зеркальном отражении). Полная четность частицы Р = π(-1) l , где π – её внутренняя четность, а (-1) l – её орбитальная четность. Внутренние четности кварков положительные, антикварков - отрицательные.
I	Изоспин. Характеризует свойство зарядовой инвариантности сильных взаимодействий

Для обозначения спинового момента часто используют букву J.

Все состояния, в которых может находиться квантовая система, описываются с помощью полного набора квантовых чисел. Так в случае протона в ядре состояние протона описывается с помощью четырех квантовых чисел, соответствующих четырем степеням свободы – трем пространственным координатам и спину. Это

• Радиальное квантовое число n (1, 2, …, ∞),
• Орбитальное квантовое число l (0, 1, 2, …),
• Проекция орбитального момента m (± l, ± (l-1), …, ±1, 0),
• Спин протона s =1/2.

Для описания сферически-симметричных систем в квантовой физике используются различные сферически симметричные потенциалы с различной радиальной зависимостью:

где U 0 , а и R – положительные константы (R – радиус ядра). Во всех случаях сферически симметричные системы можно описать с помощью набора квантовых чисел n, l, j, j z , однако, в зависимости от радиального вида потенциала энергетический спектр состояний системы будет различным.
Существование сохраняющихся во времени физических величин тесно связано со свойствами симметрии гамильтониана системы. Например, в случае, если квантовая система обладает центральной симметрией U = U(r), то этой системе соответствует сохранение орбитального момента количества движения l и одной из его проекций m. При этом из-за сферической симметрии задачи энергия состояний не будет зависеть от величины m, т. е. состояния будут вырожденными по m.
Наряду с пространственными симметриями, связанными с непрерывными преобразованиями, в квантовой физике существуют и другие симметрии – дискретные. Одной из них является зеркальная симметрия волновой функции относительно инверсии координат (→ -). Оператору инверсии соответствует квантовое число четность, которое может принимать два значения +1 и -1 в зависимости от того, сохраняется ли знак волновой функции при инверсии или меняется на противоположный.
Система тождественных частиц характеризуется еще одной симметрией – симметрией относительно перестановок тождественных частиц. Эта симметрия определяется свойствами частиц, образующих систему. Системы частиц с целым спином (бозонов) описываются симметричными волновыми функциями, системы частиц с полуцелым спином (фермионов) − антисимметричными волновыми функциями.

(Документ)

Фадеева А.А. Тренировочные задания по физике (Документ)

Решения экзаменационных билетов по физике (3 семестр, оптика, ядерная физика) (Документ)

Билеты с ответами на экзамен по физике (раздел Оптика) (Документ)

Струж Н., Чиж О. ДПА 2012. Фізика 11 клас: Розв"язки завдань державної підсумкової атестації (Документ)

(Документ)

ЕГЭ 2011 - Диагностическая работа по физике (Документ)

n1.doc

Уравнение Шредингера

Для описания поведения микрочастиц необходима особая форма механики, учитывающая их волновые свойства. Новая механика получила название волновой или квантовой механики. Основные авторы Шредингер, Гайзенберг, Дирак, Паули. Кроме того, в Копенгагене активно работала группа под общим руководством Н. Бора.

Основным уравнением квантовой механики является уравнение Шредингера. Подобно тому, как уравнения динамики Ньютона не могут быть получены теоретически, а представляют собой обобщение большого числа опытных фактов, уравнение Шредингера также нельзя вывести из каких – либо известных ранее соотношений. Его следует рассматривать как исходное основное предположение, справедливость которого доказывается тем, что все вытекающие из него следствия достаточно точно согласуются с опытными фактами.

Поскольку точное значение параметров состояния микрочастицы неизвестно, основной задачей квантовой механики является определение вероятности реализации данной величины, если она может быть измерена. Для этого, по аналогии с рассмотрением дуализма волна – квант энергии, вводится в рассмотрение функция волны, соответствующей частице (волновая функция), которую принято обозначать буквой . Она является функцией координат и времени и может быть найдена путем решения уравнения:

Это уравнение было введено в практику Шредингером в 1926 г. и называется уравнением Шредингера со временем (или временным уравнением Шредингера). Здесь: i – мнимая единица; ħ – постоянная Планка; m – масса частицы; U – потенциальная энергия частицы; ? – оператор Лапласа

Из уравнения Шредингера следует, что волновая функция определяется потенциальной энергией U , т. е., в конечном счете, есть функция координат и времени. Для стационарного силового поля U не зависит явно от времени. В этом случае волновая функция представляется в виде множителей, один из которых зависит только от времени, второй – только от координат:

где Е – полная энергия частицы.

В самом деле, при подстановке этой функции в уравнение Шредингера с независящим от времени силовым полем экспоненты, содержащие время, сокращаются. Тогда уравнение для не зависящих от времени состояний  (стационарных состояний) получает вид:

(*)

В дальнейшем мы будем называть это выражение просто уравнением Шредингера.

К уравнению Шредингера можно прийти путем следующих рассуждений. Из опытов по дифракции микрочастиц вытекает, что параллельный пучок частиц обладает свойствами плоской волны, распространяющейся в направлении движения частиц. Уравнение плоской волны, распространяющейся в направлении оси х , имеет вид:

Согласно гипотезе де – Бройля свободному движению частицы соответствует плоская волна с частотой  = E/t и длиной волны  = 2ħ/p. Подставляя  и  в уравнение плоской волны, получим волновую функцию для свободной частицы, движущейся в направлении оси х :

Продифференцировав функцию  один раз по t, a второй раз дважды по х, получим:

Из этих соотношений можно выразить Е и р 2 через функцию  и её производные:

Теперь запишем для нерелятивистского случая E = p 2 /2m и подставим в него полученные выражения:

Появление в уравнении лапласиана есть обобщение уравнения на случай распространения волны в произвольном направлении.

Полученное уравнение совпадает с уравнением Шредингера для движения свободной частицы (U = 0). Так как данное состояние стационарно (U = 0 и, следовательно, не зависит от времени) уравнение получает вид:

Это уравнение совпадает с уравнением (*) для случая U = 0.

Полная энергия Е складывается из кинетической энергии Т и потенциальной энергии U. В случае свободной частицы полная энергия Е совпадает с кинетической Т, так что величину Е можно трактовать либо как полную, либо как кинетическую энергию частицы. Если принять, что Е – полная энергия частицы получится не физичная ситуация: обобщенное уравнение не будет зависеть от характера силового поля (то есть от U). Поэтому при наличии сил, действующих на частицу, вместо Е в уравнение нужно ввести кинетическую энергию частицы Т = Е– U. Произведя такую замену, мы придем к уравнению (*).

Еще раз отметим, что приведенные математические манипуляции не могут рассматриваться как вывод уравнения Шредингера. Их цель – пояснить, каким образом можно было прийти к установлению вида волнового уравнения для микрочастицы. Доказательством же правильности уравнения Шредингера может служить лишь согласие с опытом тех результатов, которые получаются с помощью этого уравнения.

Квантование энергии.

В отличие от модели атома Бора, основанной на введении некоторых постулатов, уравнение Шредингера позволяет получить фиксированные значения энергии при непосредственном решении уравнения. Требования, предъявляемые к волновым функциям вполне стандартны для математики: конечность, однозначность, непрерывность, гладкость. Требования должны выполняться даже в случае неаналитического поведения потенциала U: потенциал может быть разрывным, бесконечным в некоторой области пространства и проч.

Решения, получаемые при этом, соответствуют лишь некоторым определённым значениям энергии Е. Они носят название собственных значений энергии. Волновые функции, полученные в процессе решения уравнения Шредингера, носят название собственных функций, принадлежащих собственным значениям.

Значения Е могут быть как дискретными (квантованными), так и принимать непрерывный набор значений. В последнем случае говорят о непрерывном спектре энергии.

Решив уравнение Шредингера, вообще говоря, можно получить и набор вероятностей обнаружения других параметров частицы: импульса и момента импульса.

Наконец, следует отметить некоторую ограниченность полученных решений. Она заключается в том, что стационарное уравнение Шредингера не предназначено для рассмотрения процессов во времени. Между тем, опыт показывает, что энергии стационарных (точнее почти стационарных) состояний получаются в полном согласии с опытом.

Частица в потенциальной яме .

Решение задач о поведении или состоянии частицы в потенциальной яме позволяет продемонстрировать математическую сторону квантового подхода. Кроме того, потенциальная яма является отличной моделью для получения представления о формировании энергетического спектра частиц, ограниченных в своём движении. С точки зрения атомной или ядерной теории имеет смысл рассмотреть частицу в ямах трёх типов. Простейший случай – частица в прямоугольной потенциальной яме с бесконечно высокими стенками есть всего лишь пример решения задачи в квантовой теории и демонстрация универсального факта появления дискретных состояний микрочастицы, ограниченной в своём движении. Рассмотрение состояния частицы в яме с параболическим потенциалом позволяет понять особенности колебаний связанных микрочастиц и решение этой задачи имеет прямое отношение к расчёту теплоёмкости твёрдого тела. Наконец, решение задачи с гиперболической ямой аналогично решению задачи о состояниях электрона в атоме водорода, но без использования гипотезы о существовании стационарных состояний. В данном случае стационарность состояний есть следствие решения задачи (уравнения Шредингера).

Рассмотрим поведение частицы в бесконечно глубокой прямоугольной потенциальной яме .

Для простоты примем, что частица движется вдоль оси х (см. рисунок). В пределах 0  х  l потенциал U = 0. Вне этих пределов потенциал бесконечен: U  . Фактически это означает, что вне пределов ямы функция равна нулю, так как частица вне ямы существовать не может. Тогда для 0  х  l можем написать:

Общее решение этого уравнения имеет вид:

Как говорилось выше,  (х = 0) =  (х = l ) = 0. Первое равенство позволяет определить  = 0. Из второго следует, что  l = n  . Определив отсюда  и подставив это значение в выражение для  2 , получим собственные значения задачи:

Заметим, что n = 1,2,3…, но не равно нулю, так как при этом исчезает волновая функция: частица отсутствует. Собственные функции определяются тогда таким образом:

Функции определены с точностью до постоянного множителя а . В подавляющем большинстве случаев бывает удобным, чтобы функция была нормирована. При этом имеется ввиду, что интеграл от плотности вероятности
нахождения частицы во всех возможных состояниях равен единице. (Звёздочка означает комплексное сопряжение). Условие нормировки соответствует достоверности нахождения частицы в одном из возможных состояний. Формально это равносильно определению коэффициента при волновой функции:

Волновая функция приобрела полный вид:

Теперь можно определить распределение плотности вероятности нахождения электрона по координате х :

Графики распределения волновой функции и плотности вероятности приведены на рисунке. Очевидно, что график распределения вероятности соответствует распределению интенсивности стоячей волны. Обращает на себя внимание аномальность распределения вероятности при малых значениях числа n : частица пребывает в основном в середине интервала возможных положений. Однако при очень больших n вероятность появления частицы вблизи стенки растёт, то есть при больших n частица становится подобной классической.

Частица в параболической яме .

Часто эта задача называется задачей о квантовом осцилляторе, так как в ней рассматривается вопрос о колебаниях микрочастицы. В квантовой физике понятие силы теряет свой смысл из-за проявления соотношения неопределённости координата – импульс. В этом случае использование уравнения Шредингера позволяет решить задачу о колебаниях частицы, обладающей потенциальной энергией аналогичной потенциальной энергии в классической теории:

Так как в классической механике действие упругой силы проявляется в существовании собственной частоты
, имеет смысл перейти к выражению:

Здесь жёсткость определена из выражения для собственной частоты колебаний. Тогда уравнение Шредингера приобретает вид:

Математическое решение этого уравнения весьма громоздко и требует применения так называемых специальных функций. Поэтому укажем, что требования к собственным функциям данной задачи (непрерывность, гладкость, конечность, однозначность) выполняются при собственных значениях задачи:

Е = ħ  ( + 1/2), ( = 0,1,2,…)

Эти энергии для различных  (цифры справа) вместе с зависимостью потенциальной энергии от координаты х (жирная сплошная линия) приведены на рисунке.

Из полученного выражения следует, что уровни осциллятора эквидистантны. Энергия, соответствующая  = 0 носит название нулевой энергии колебаний. Её появление уже объяснено выше действием принципа неопределённости: частица не может покоиться и одновременно иметь некоторую координату в данном случае равную нулю.

Изменение введённого квантового числа  возможно только на единицу? =  1. Это так называемое правило отбора для гармонического квантового осциллятора. Подобное изменение появляется, например, при оптических переходах между стационарными состояниями, обусловленными взаимодействием электронов атома с ядром и друг с другом. Приведённая картина характеризует спектр в каждом из стационарных состояний электронов атома. При переходах с изменением числа  помимо прочего испускается квант с энергией ħ, где частота  приобретает свой реальный физический смысл.

Говорить о частоте колебаний частицы в каждом стационарном состоянии неверно. Частица в классическом осцилляторе может двигаться лишь в пределах координаты, задаваемых потенциальной кривой. При падении её на границу она отражается. Микрочастица в квантовой механике может проникать внутрь соседней области, то есть за границу потенциальной кривой. При этом о колебаниях не может быть никакой речи. Имеет смысл только плотность вероятности нахождения частицы в некоторой точке.

На рисунке приведено распределение плотности вероятности обнаружения частицы в параболической потенциальной яме вдоль оси Х . Жирные горизонтальные линии есть расстояние между классическими “точками поворота” частицы, находящимися на потенциальной кривой и соответствующими разным значениям числа  . Видно, что проникновение частицы в соседнюю область тем меньше, чем больше значение числа  , то есть частица становится более классической при увеличении её полной энергии.

Потенциальные барьеры .

Рассмотрим движение частицы в области пространства, содержащей потенциальный барьер. Примером физической ситуации, в которой проявляется действие барьера на движение частицы, может служить выход электрона за пределы твёрдого тела (автоэлектронная эмиссия). Зависимость формы барьера от координат может быть весьма сложной, но высота барьера конечна и, как правило, вполне конечна длина нарастания барьера. Поэтому в качестве простой модельной задачи следует взять барьер высоты U 0

с вертикальной стенкой. Соответственно, потенциальная энергия будет представлена в виде:

Пусть частица налетает на барьер с левой стороны. Частицу, как обычно, рассматриваем как волну де-Бройля:

Задача заключается в определении амплитуды волны, а затем в определении коэффициентов её отражения и прохождения. Существование отражённой и прошедшей волн возникает из требований, накладываемых на вид функции и её производной (гладкость, однозначность, непрерывность, конечность) при х = 0.

Частота падающей, отражённой и прошедшей волн должна быть одной и той же. Это позволяет перейти от время зависимой функции к функции, зависящей только от координат. Для этого достаточно подставить функцию (x,t) в общее уравнение Шредингера, сократить экспоненту, зависящую от времени и получить стационарное уравнение Шредингера:

В данной задаче имеются два варианта рассмотрения E 1 >U 0 и E 2
1. E 1 >U 0 . Общий вид решения имеет вид

Амплитуда падающей волны равна а 1 , отражённой b 1 . В области x>0 волна только прошедшая (слева направо), поэтому b 2 = 0. Из условия непрерывности и гладкости при х = 0 получаем:

Отсюда получаем:

Для определения коэффициентов прохождения D и отражения R необходимо ввести понятие потока плотности вероятности F . В данном случае оно аналогично обычному понятию потока, применённому к распространению волны: это энергия потока в единицу времени, равная произведению плотности энергии на скорость распространения. Энергия волны пропорциональна квадрату её амплитуды. В рассматриваемом случае скорость потока равна скорости движения частицы. Последняя равна  = р /m = ħ k /m . Тогда:

Обозначим: F – поток падающей волны, F’ поток отражённой волны, F” – поток прошедшей волны. Получаем искомый результат:

Особенности полученного результата:

1. Сумма коэффициентов прохождения и отражения равна единице, что вполне стандартно.

2. Коэффициенты не зависят от направления движения частицы – волны.

3. Даже при энергии частицы большей высоты потенциальной ступеньки существует отражение частицы от барьера.

1. E 1 оказывается мнимой величиной k 2 = ik . Тогда отражение частицы от барьера полное, то есть R = 1.

Вместе с тем, легко видеть, что функция прошедшей во вторую область волны не равна нулю. Так как
функция прошедшей волны равна

Плотность вероятности, таким образом, пропорциональна отрицательной вещественной экспоненте, то есть быстро затухает по мере распространения волны вглубь барьера:

Глубину проникновения l определяют как расстояние при котором величина Р уменьшается в е раз. Тогда 2kl =1. Отсюда

Отсюда следует, например, что при U 0 -E = 10 -3 эВ электрон проникает вглубь барьера на 10 -9 м.

Таким образом, при набегании частицы на потенциальную стенку достаточно малой толщины возможно проникновение этой частицы сквозь стенку как бы по туннелю, что определило название этого явления: туннельный эффект . Разумеется, такое проникновение возможно лишь с определённой вероятностью, что, тем не менее, позволяет не только регистрировать эффект, но и использовать его в практике. Существует так называемый туннельный диод, обладающий рядом весьма интересных характеристик.

В физике, помимо холодной эмиссии электронов из металла, действием туннельного эффекта объясняется  - распад, спонтанное деление ядер, термоядерный синтез и целый ряд других явлений.

Операторы физических величин .

Зная волновую функцию, можно определить любые измеряемые характеристики микрочастицы. Для этого пользуются своеобразным исчислением, носящим название операционного. Чтобы понять суть операционного исчисления, определим вначале очень важное в квантовой механике понятие среднего значения. Рассмотрим для начала координату и определим вероятность dP нахождения частицы в области dx в окрестности точки х. В соответствии с изложенным выше dP = *dx. Тогда среднее значение координаты х равно

При этом предполагается, что функция  нормирована:

Аналогично можно определить среднее значение любой величины, зависящей от координаты:

Для получения других величин приходится проводить дополнительные расчеты, порой весьма громоздкие, позволившие получить, например, среднее значение импульса:

Если записать приведённые выражения в виде:

то оказывается, что получение средних значений можно связать с действием на волновую функцию некоторого оператора. Тип действия и вид оператора подчиняются следующему правилу: формулы классической физики для связи между величинами в квантовой теории заменяются формулами, связывающими операторы этих величин .

Например, оператором координаты или величины f(x) в приведённом выражении являются сами величины. Их действие заключается в умножении этих величин на функцию . Оператор импульса дифференциальный и имеет вид (ср. с последним выражением):

Обозначаются операторы символами величин, но со шляпкой наверху. Например, оператор импульса записывается в виде .

Основные математические свойства операторов :

1. Операторы можно складывать (ассоциативность). Действие суммы операторов равно сумме их действий порознь: . Здесь символ  обозначает аргумент функции f .

2. Операторы можно перемножать. Действие произведения операторов равно последовательному применению операторов к функции:
. Здесь следует отметить, что коммутативность операторов не является их общим свойством, то есть
может быть не равно
. Если всё-таки равенство выполняется, то операторы называются коммутирующими. Можно показать, что всегда не коммутируют операторы величин, входящих в соотношения неопределённости. Справедливо и обратное соответствие: если операторы не коммутируют, то соответствующие им величины не могут быть определены одновременно.

3. Операторы называются линейными, если выполняется условие:

Именно линейность операторов определяет возможность использования принципа суперпозиции волн де-Бройля.

Приведённые примеры можно обобщить. Среднее значение величины Q равно:

где есть оператор величины Q .

Рассмотрим операторы основных физических величин.

По аналогии с введённым выше оператором проекции импульса можно написать:

Отсюда оператор квадрата импульса имеет вид:

Теперь можно написать оператор энергии, один из основных операторов квантовой механики. Кинетическая энергия определяется в соответствии с приведённым правилом:

Оператор полной энергии, так называемый оператор Гамильтона или гамильтониан, получает уже известный, использованный выше, вид:

Теперь можно определить среднее значение полной энергии, действуя на волновую функцию оператором Гамильтона:

Несмотря на невозможность одновременного определения потенциальной и кинетической энергии можно определить и сопоставить сумму средних значений этих энергий среднему значению полной энергии.

Таким образом, если известна волновая функция частицы, всегда можно определить среднее значение соответствующей величины.

Роль операторов в квантовой механике будет определена не полностью, если не сформулировать общее соотношение, позволяющее получить расчётным путём собственное значение любой величины Q . Это соотношение имеет вид:

(*)

В его справедливости можно убедиться, рассчитывая среднее значение величины Q :

В данном случае волновая функция является собственной функцией задачи или оператора . Значение Q в рассмотренном случае единственное (поэтому собственное). Других значений, соответствующих данной функции, нет. Взаимное соответствие функции и значения в виде (*) есть определение собственных функций и собственных значений опрератора .

Примером соответствия выражения (*) предыдущим уравнениям движения частиц является его совпадение со стационарным уравнением Шредингера. Подставив оператор Гамильтона в уравнение (*), получим уравнение Шредингера для стационарных состояний:

Квантование момента импульса.

В квантовой механике свойства момента импульса существенно отличаются от свойств этой же величины в классической теории. Например, существенной величиной является не сам вектор, а модуль момента М или квадрат момента импульса М 2 . Исследование коммутационных свойств операторов показывает, что коммутируют только квадрат момента и одна из его проекций. Обычно она соотносится с осью Z. Две другие проекции и квадрат момента М 2 друг с другом не коммутируют. Как было сказано выше, это означает возможность одновременного определения только двух данных величин М 2 и М z . Поэтому можно представить, что момент образован некоторым неопределённым движением вектора по конусу. Тогда определимы только проекция и длина вектора.

Следуя приведённому выше правилу, можно ввести в рассмотрение оператор момента импульса . В классической механике момент импульса равен

Тогда оператор проекции момента импульса на ось Z равен

Более простой вид он приобретает в сферической системе координат (r, , ):

Квадрат момента импульса определяется общим уравнением:

В силу большого объема рассуждений и вычислений приведём конечный результат решения этого уравнения:

Число l называется орбитальным квантовым числом. Отсюда модуль момента импульса равен:

В отличие от классического момента квантовый его аналог не зависит от положения точки, относительно которой он определяется. Он определяется только угловым движением частицы. Поэтому в квантовой механике часто момент импульса называется угловым моментом или просто моментом. То же относится и к собственным значениям оператора проекции момента.
вырождении энергетического состояния . Это связано с произвольностью выбора оси Z в отсутствии магнитного поля. Введение в рассмотрение электрического поля не позволяет выбрать направление оси, поэтому электрическое поле снять вырождение по проекции момента полностью не может. Остаётся как минимум двукратное вырождение.

Вообще кратность вырождения проекции момента определяется тем, что формально M z есть проекция момента и, следовательно, не может по величине превышать величину М . Отсюда следует, что

Общее число значений m равно, таким образом, 2l +1, что и определяет кратность вырождения орбитальных состояний.

Полученные результаты можно представить хорошо известным образом:

Они представляют суть положения, называемого пространственным квантованием .