Тригонометрические уравнения. Исчерпывающее руководство (2019)

Чтобы успешно решать тригонометрические уравнения удобно пользоваться методом сведения к ранее решенным задачам. Давайте разберемся, в чем суть этого метода?

В любой предлагаемой задаче вам необходимо увидеть уже решенную ранее задачу, а затем с помощью последовательных равносильных преобразований попытаться свести данную вам задачу к более простой.

Так, при решении тригонометрических уравнений обычно составляют некоторую конечную последовательность равносильных уравнений, последним звеном которой является уравнение с очевидным решением. Только важно помнить, что если навыки решения простейших тригонометрических уравнений не сформированы, то решение более сложных уравнений будет затруднено и малоэффективно.

Кроме того, решая тригонометрические уравнения, никогда не стоит забывать о возможности существования нескольких способов решения.

Пример 1. Найти количество корней уравнения cos x = -1/2 на промежутке .

Решение:

I способ. Изобразим графики функций y = cos x и y = -1/2 и найдем количество их общих точек на промежутке (рис. 1).

Так как графики функций имеют две общие точки на промежутке , то уравнение содержит два корня на данном промежутке.

II способ. С помощью тригонометрического круга (рис. 2) выясним количество точек, принадлежащих промежутку , в которых cos x = -1/2. По рисунку видно, что уравнение имеет два корня.

III способ. Воспользовавшись формулой корней тригонометрического уравнения, решим уравнение cos x = -1/2.

x = ± arccos (-1/2) + 2πk, k – целое число (k € Z);

x = ± (π – arccos 1/2) + 2πk, k – целое число (k € Z);

x = ± (π – π/3) + 2πk, k – целое число (k € Z);

x = ± 2π/3 + 2πk, k – целое число (k € Z).

Промежутку принадлежат корни 2π/3 и -2π/3 + 2π, k – целое число. Таким образом, уравнение имеет два корня на заданном промежутке.

Ответ: 2 .

В дальнейшем тригонометрические уравнения будут решаться одним из предложенных способов, что во многих случаях не исключает применения и остальных способов.

Пример 2. Найти количество решений уравнения tg (x + π/4) = 1 на промежутке [-2π; 2π].

Решение:

Воспользовавшись формулой корней тригонометрического уравнения, получим:

x + π/4 = arctg 1 + πk, k – целое число (k € Z);

x + π/4 = π/4 + πk, k – целое число (k € Z);

x = πk, k – целое число (k € Z);

Промежутку [-2π; 2π] принадлежат числа -2π; -π; 0; π; 2π. Итак, уравнение имеет пять корней на заданном промежутке.

Ответ: 5.

Пример 3. Найти количество корней уравнения cos 2 x + sin x · cos x = 1 на промежутке [-π; π].

Решение:

Так как 1 = sin 2 x + cos 2 x (основное тригонометрическое тождество), то исходное уравнение принимает вид:

cos 2 x + sin x · cos x = sin 2 x + cos 2 x;

sin 2 x – sin x · cos x = 0;

sin x(sin x – cos x) = 0. Произведение равно нулю, а значит хотя бы один из множителей должен быть равен нулю, поэтому:

sin x = 0 или sin x – cos x = 0.

Так как значение переменной, при которых cos x = 0, не являются корнями второго уравнения (синус и косинус одного и того же числа не могут одновременно быть равными нулю), то разделим обе части второго уравнения на cos x:

sin x = 0 или sin x / cos x - 1 = 0.

Во втором уравнении воспользуемся тем, что tg x = sin x / cos x, тогда:

sin x = 0 или tg x = 1. С помощью формул имеем:

x = πk или x = π/4 + πk, k – целое число (k € Z).

Из первой серии корней промежутку [-π; π] принадлежат числа -π; 0; π. Из второй серии: (π/4 – π) и π/4.

Таким образом, пять корней исходного уравнения принадлежат промежутку [-π; π].

Ответ: 5.

Пример 4. Найти сумму корней уравнения tg 2 x + сtg 2 x + 3tg x + 3сtgx + 4 = 0 на промежутке [-π; 1,1π].

Решение:

Перепишем уравнение в следующем виде:

tg 2 x + сtg 2 x + 3(tg x + сtgx) + 4 = 0 и сделаем замену.

Пусть tg x + сtgx = a. Обе части равенства возведем в квадрат:

(tg x + сtg x) 2 = a 2 . Раскроем скобки:

tg 2 x + 2tg x · сtgx + сtg 2 x = a 2 .

Так как tg x · сtgx = 1, то tg 2 x + 2 + сtg 2 x = a 2 , а значит

tg 2 x + сtg 2 x = a 2 – 2.

Теперь исходное уравнение имеет вид:

a 2 – 2 + 3a + 4 = 0;

a 2 + 3a + 2 = 0. С помощью теоремы Виета получаем, что a = -1 или a = -2.

Сделаем обратную замену, имеем:

tg x + сtgx = -1 или tg x + сtgx = -2. Решим полученные уравнения.

tg x + 1/tgx = -1 или tg x + 1/tgx = -2.

По свойству двух взаимно обратных чисел определяем, что первое уравнение не имеет корней, а из второго уравнения имеем:

tg x = -1, т.е. x = -π/4 + πk, k – целое число (k € Z).

Промежутку [-π; 1,1π] принадлежат корни: -π/4; -π/4 + π. Их сумма:

-π/4 + (-π/4 + π) = -π/2 + π = π/2.

Ответ: π/2.

Пример 5. Найти среднее арифметическое корней уравнения sin 3x + sin x = sin 2x на промежутке [-π; 0,5π].

Решение:

Воспользуемся формулой sin α + sin β = 2sin ((α + β)/2) · cos ((α – β)/2), тогда

sin 3x + sin x = 2sin ((3x + x)/2) · cos ((3x – x)/2) = 2sin 2x · cos x и уравнение принимает вид

2sin 2x · cos x = sin 2x;

2sin 2x · cos x – sin 2x = 0. Вынесем общий множитель sin 2x за скобки

sin 2x(2cos x – 1) = 0. Решим полученное уравнение:

sin 2x = 0 или 2cos x – 1 = 0;

sin 2x = 0 или cos x = 1/2;

2x = πk или x = ±π/3 + 2πk, k – целое число (k € Z).

Таким образом, имеем корни

x = πk/2, x = π/3 + 2πk, x = -π/3 + 2πk, k – целое число (k € Z).

Промежутку [-π; 0,5π] принадлежат корни -π; -π/2; 0; π/2 (из первой серии корней); π/3 (из второй серии); -π/3 (из третьей серии). Их среднее арифметическое равно:

(-π – π/2 + 0 + π/2 + π/3 – π/3)/6 = -π/6.

Ответ: -π/6.

Пример 6. Найти количество корней уравнения sin x + cos x = 0 на промежутке [-1,25π; 2π].

Решение:

Данное уравнение является однородным уравнением первой степени. Разделим обе его части на cosx (значение переменной, при которых cos x = 0, не являются корнями данного уравнения, так как синус и косинус одного и того же числа не могут одновременно быть равными нулю). Исходное уравнение имеет вид:

x = -π/4 + πk, k – целое число (k € Z).

Промежутку [-1,25π; 2π] принадлежат корни -π/4; (-π/4 + π); и (-π/4 + 2π).

Таким образом, заданному промежутку принадлежат три корня уравнения.

Ответ: 3.

Научитесь делать самое главное – четко представлять план решения задачи, и тогда любое тригонометрическое уравнение будет вам по плечу.

Остались вопросы? Не знаете, как решать тригонометрические уравнения?
Чтобы получить помощь репетитора – зарегистрируйтесь .

сайт, при полном или частичном копировании материала ссылка на первоисточник обязательна.

Тригонометрические уравнения. В составе экзамена по математике в первой части имеется задание связанное с решением уравнения — это простые уравнения, которые решаются за минуты, многие типы можно решить устно. Включают в себя: линейные, квадратные, рациональные, иррациональные, показательные, логарифмические и тригонометрические уравнения.

В этой статье мы рассмотрим тригонометрические уравнения. Их решение отличается и по объёму вычисления и по сложности от остальных задач этой части. Не пугайтесь, под словом «сложность», имеется виду их относительную сложность по сравнению с другими заданиями.

Кроме нахождения самих корней уравнения, необходимо определить наибольший отрицательный, либо наименьший положительный корень. Вероятность того, что вам на экзамене попадёт тригонометрическое уравнение, конечно же, мала.

Их в данной части ЕГЭ менее 7%. Но это не означает, что их нужно оставить без внимания. В части С тоже необходимо решить тригонометрическое уравнение, поэтому хорошо разобраться с методикой решения и понимать теорию просто необходимо.

Понимание раздела «Тригонометрия» в математике во многом определяет ваш успех при решении многих задач. Напоминаю, что ответом является целое число или конечная десятичная дробь. После того, как получите корни уравнения, ОБЯЗАТЕЛЬНО сделайте проверку. Много времени это не займёт, а вас избавит от ошибки.

В будущем мы также рассмотрим и другие уравнения, не пропустите! Вспомним формулы корней тригонометрических уравнений, их необходимо знать:

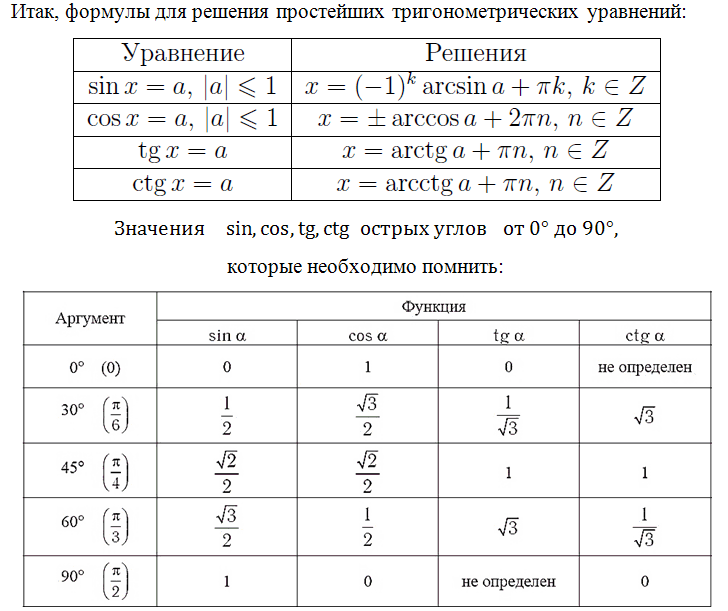
Знание этих значений необходимо, это «азбука», без которой невозможно будет справиться с множеством заданий. Отлично, если память хорошая, вы легко выучили и запомнили эти значения. Что делать, если этого сделать не получается, в голове путаница, да просто вы именно при сдаче экзамена сбились. Обидно будет потерять бал из-за того, что вы запишите при расчётах неверное значение.

Этих значений прост, он также приведён в теории, полученной вами во втором письме после подписки на рассылку. Если ещё не подписались, сделайте это! В будущем также рассмотрим, как эти значения можно определить по тригонометрической окружности. Не даром её называют «Золотое сердце тригонометрии».

Сразу поясню, во избежание путаницы, что в рассматриваемых ниже уравнениях даны определения арксинуса, арккосинуса, арктангенса с использованием угла х для соответствующих уравнений: cosx=a, sinx=a, tgx=a, где х может быть и выражением. В примерах ниже у нас аргумент задан именно выражением.

Итак, рассмотрим следующие задачи:

Найдите корень уравнения:

В ответе запишите наибольший отрицательный корень.

Решением уравнения cos x = a являются два корня:

Определение: Пусть число a по модулю не превосходит единицы. Арккосинусом числа a называется угол x, лежащий в пределах от 0 до Пи, косинус которого равен a.

Значит

Выразим x :

Найдём наибольший отрицательный корень. Как это сделать? Подставим различные значения n в полученные корни, вычислим и выберем наибольший отрицательный.

Вычисляем:

При n = – 2 х 1 = 3 (– 2) – 4,5 = – 10,5 х 2 = 3 (– 2) – 5,5 = – 11,5

При n = – 1 х 1 = 3 (– 1) – 4,5 = – 7,5 х 2 = 3 (– 1) – 5,5 = – 8,5

При n = 0 х 1 = 3∙0 – 4,5 = – 4,5 х 2 = 3∙0 – 5,5 = – 5,5

При n = 1 х 1 = 3∙1 – 4,5 = – 1,5 х 2 = 3∙1 – 5,5 = – 2,5

При n = 2 х 1 = 3∙2 – 4,5 = 1,5 х 2 = 3∙2 – 5,5 = 0,5

Получили, что наибольший отрицательный корень равен –1,5

Ответ: –1,5

Решите самостоятельно:

Решите уравнение:

Решением уравнения sin x = a являются два корня:

Либо (он объединяет оба указанные выше):

Определение: Пусть число a по модулю не превосходит единицы. Арксинусом числа a называется угол x, лежащий в пределах от – 90 о до 90 о синус которого равен a.

Значит

Выразим x (умножим обе части уравнения на 4 и разделим на Пи):

Найдём наименьший положительный корень. Здесь сразу видно, что при подстановке отрицательных значений n мы получим отрицательные корни. Поэтому будем подставлять n = 0,1,2 …

При n = 0 х = (– 1) 0 + 4∙0 + 3 = 4

При n = 1 х = (– 1) 1 + 4∙1 + 3 = 6

При n = 2 х = (– 1) 2 + 4∙2 + 3 = 12

Проверим при n = –1 х = (–1) –1 + 4∙(–1) + 3 = –2

Значит наименьший положительный корень равен 4.

Ответ: 4

Решите самостоятельно:

Решите уравнение:

В ответе напишите наименьший положительный корень.

Соблюдение Вашей конфиденциальности важно для нас. По этой причине, мы разработали Политику Конфиденциальности, которая описывает, как мы используем и храним Вашу информацию. Пожалуйста, ознакомьтесь с нашими правилами соблюдения конфиденциальности и сообщите нам, если у вас возникнут какие-либо вопросы.

Сбор и использование персональной информации

Под персональной информацией понимаются данные, которые могут быть использованы для идентификации определенного лица либо связи с ним.

От вас может быть запрошено предоставление вашей персональной информации в любой момент, когда вы связываетесь с нами.

Ниже приведены некоторые примеры типов персональной информации, которую мы можем собирать, и как мы можем использовать такую информацию.

Какую персональную информацию мы собираем:

• Когда вы оставляете заявку на сайте, мы можем собирать различную информацию, включая ваши имя, номер телефона, адрес электронной почты и т.д.

Как мы используем вашу персональную информацию:

• Собираемая нами персональная информация позволяет нам связываться с вами и сообщать об уникальных предложениях, акциях и других мероприятиях и ближайших событиях.
• Время от времени, мы можем использовать вашу персональную информацию для отправки важных уведомлений и сообщений.
• Мы также можем использовать персональную информацию для внутренних целей, таких как проведения аудита, анализа данных и различных исследований в целях улучшения услуг предоставляемых нами и предоставления Вам рекомендаций относительно наших услуг.
• Если вы принимаете участие в розыгрыше призов, конкурсе или сходном стимулирующем мероприятии, мы можем использовать предоставляемую вами информацию для управления такими программами.

Раскрытие информации третьим лицам

Мы не раскрываем полученную от Вас информацию третьим лицам.

Исключения:

• В случае если необходимо - в соответствии с законом, судебным порядком, в судебном разбирательстве, и/или на основании публичных запросов или запросов от государственных органов на территории РФ - раскрыть вашу персональную информацию. Мы также можем раскрывать информацию о вас если мы определим, что такое раскрытие необходимо или уместно в целях безопасности, поддержания правопорядка, или иных общественно важных случаях.
• В случае реорганизации, слияния или продажи мы можем передать собираемую нами персональную информацию соответствующему третьему лицу – правопреемнику.

Защита персональной информации

Мы предпринимаем меры предосторожности - включая административные, технические и физические - для защиты вашей персональной информации от утраты, кражи, и недобросовестного использования, а также от несанкционированного доступа, раскрытия, изменения и уничтожения.

Соблюдение вашей конфиденциальности на уровне компании

Для того чтобы убедиться, что ваша персональная информация находится в безопасности, мы доводим нормы соблюдения конфиденциальности и безопасности до наших сотрудников, и строго следим за исполнением мер соблюдения конфиденциальности.

Решение простейших тригонометрических уравнений.

Решение тригонометрических уравнений любого уровня сложности в конечном итоге сводится к решению простейших тригонометрических уравнений. И в этом наилучшим помощником снова оказывается тригонометрический круг.

Вспомним определения косинуса и синуса.

Косинусом угла называется абсцисса (то есть координата по оси ) точки на единичной окружности, соответствующей повороту на данный угол .

Синусом угла называется ордината (то есть координата по оси ) точки на единичной окружности, соответствующей повороту на данный угол .

Положительным направлением движения по тригонометрическому кругу считается движение против часовой стрелки. Повороту на 0 градусов (или 0 радиан) соответствует точка с координатами (1;0)

Используем эти определения для решения простейших тригонометрических уравнений.

1. Решим уравнение

Этому уравнению удовлетворяют все такие значения угла поворота , которые соответствуют точкам окружности, ордината которых равна .

Отметим на оси ординат точку с ординатой :

Проведем горизонтальную линию параллельно оси абсцисс до пересечения с окружностью. Мы получим две точки, лежащие на окружности и имеющие ординату . Эти точки соответствуют углам поворота на и радиан:

Если мы, выйдя из точки, соответствующей углу поворота на радиан, обойдем полный круг, то мы придем в точку, соответствующую углу поворота на радиан и имеющую ту же ординату. То есть этот угол поворота также удовлетворяет нашему уравнению. Мы можем делать сколько угодно "холостых" оборотов, возвращаясь в ту же точку, и все эти значения углов будут удовлетворять нашему уравнению. Число "холостых" оборотов обозначим буквой (или ). Так как мы можем совершать эти обороты как в положительном, так и в отрицательном направлении, (или ) могут принимать любые целые значения.

То есть первая серия решений исходного уравнения имеет вид:

, , - множество целых чисел (1)

Аналогично, вторая серия решений имеет вид:

, где , . (2)

Как вы догадались, в основе этой серии решений лежит точка окружности, соответствующая углу поворота на .

Эти две серии решений можно объединить в одну запись:

Если мы в этой записи возьмем (то есть четное ), то мы получим первую серию решений.

Если мы в этой записи возьмем (то есть нечетное ), то мы получим вторую серию решений.

2. Теперь давайте решим уравнение

Так как - это абсцисса точки единичной окружности, полученной поворотом на угол , отметим на оси точку с абсциссой :

Проведем вертикальную линию параллельно оси до пересечения с окружностью. Мы получим две точки, лежащие на окружности и имеющие абсциссу . Эти точки соответствуют углам поворота на и радиан. Вспомним, что при движении по часовой стрелки мы получаем отрицательный угол поворота:

Запишем две серии решений:

,

,

(Мы попадаем в нужную точку, пройдя из основной полный круг, то есть .

Объедим эти две серии в одну запись:

3. Решим уравнение

Линия тангенсов проходит через точку с координатами (1,0) единичной окружности параллельно оси OY

Отметим на ней точку, с ординатой равной 1 (мы ищем, тангенс каких углов равен 1):

Соединим эту точку с началом координат прямой линией и отметим точки пересечения прямой с единичной окружностью. Точки пересечения прямой и окружности соответствуют углам поворота на и :

Так как точки, соответствующие углам поворота, которые удовлетворяют нашему уравнению, лежат на расстоянии радиан друг от друга, то мы можем записать решение таким образом:

4. Решим уравнение

Линия котангенсов проходит через точку с координатами единичной окружности параллельно оси .

Отметим на линии котангенсов точку с абсциссой -1:

Соединим эту точку с началом координат прямой и продолжим ее до пересечения с окружностью. Эта прямая пересечет окружность в точках, соответствующих углам поворота на и радиан:

Поскольку эти точки отстоят друг от друга на расстояние, равное , то общее решение этого уравнения мы можем записать так:

В приведенных примерах, иллюстрирующих решение простейших тригонометрических уравнений были использованы табличные значения тригонометрических функций.

Однако, если в правой части уравнения стоит не табличное значение, то мы в общее решение уравнения подставляем значение :

ОСОБЫЕ РЕШЕНИЯ:

Отметим на окружности точки, ордината которых равна 0:

Отметим на окружности единственную точку, ордината которой равна 1:

Отметим на окружности единственную точку, ордината которой равна -1:

Так как принято указывать значения, наиболее близкие у нулю, решение запишем так:

Отметим на окружности точки, абсцисса которых равна 0:

5.
Отметим на окружности единственную точку, абсцисса которой равна 1:

Отметим на окружности единственную точку, абсцисса которой равна -1:

И чуть более сложные примеры:

1.

Синус равен единице, если аргумент равен

Аргумент у нашего синуса равен , поэтому получим:

Разделим обе части равенства на 3:

Ответ:

2.

Косинус равен нулю, если аргумент косинуса равен

Аргумент у нашего косинуса равен , поэтому получим:

Выразим , для этого сначала перенесем вправо с противоположным знаком:

Упростим правую часть:

Разделим обе части на -2:

Заметим, что перед слагаемым знак не меняется, поскольку k может принимать любые целые значения.

Ответ:

И в заключение посмотрите видеоурок "Отбор корней в тригонометрическом уравнении с помощью тригонометрической окружности"

На этом разговор о решении простейших тригонометрических уравнений мы закончим. Следующий раз мы с вами поговорим о том, как решать .

Вы можете заказать подробное решение вашей задачи !!!

Равенство, содержащее неизвестную под знаком тригонометрической функции (`sin x, cos x, tg x` или `ctg x`), называется тригонометрическим уравнением, именно их формулы мы и рассмотрим дальше.

Простейшими называются уравнения `sin x=a, cos x=a, tg x=a, ctg x=a`, где `x` — угол, который нужно найти, `a` — любое число. Запишем для каждого из них формулы корней.

1. Уравнение `sin x=a`.

При `|a|>1` не имеет решений.

При `|a| \leq 1` имеет бесконечное число решений.

Формула корней: `x=(-1)^n arcsin a + \pi n, n \in Z`

2. Уравнение `cos x=a`

При `|a|>1` — как и в случае с синусом, решений среди действительных чисел не имеет.

При `|a| \leq 1` имеет бесконечное множество решений.

Формула корней: `x=\pm arccos a + 2\pi n, n \in Z`

Частные случаи для синуса и косинуса в графиках.

3. Уравнение `tg x=a`

Имеет бесконечное множество решений при любых значениях `a`.

Формула корней: `x=arctg a + \pi n, n \in Z`

4. Уравнение `ctg x=a`

Также имеет бесконечное множество решений при любых значениях `a`.

Формула корней: `x=arcctg a + \pi n, n \in Z`

Формулы корней тригонометрических уравнений в таблице

Для синуса:
Для косинуса:
Для тангенса и котангенса:
Формулы решения уравнений, содержащих обратные тригонометрические функции:

Методы решения тригонометрических уравнений

Решение любого тригонометрического уравнения состоит из двух этапов:

• с помощью преобразовать его до простейшего;
• решить полученное простейшее уравнение, используя выше написанные формулы корней и таблицы.

Рассмотрим на примерах основные методы решения.

Алгебраический метод.

В этом методе делается замена переменной и ее подстановка в равенство.

Пример. Решить уравнение: `2cos^2(x+\frac \pi 6)-3sin(\frac \pi 3 — x)+1=0`

`2cos^2(x+\frac \pi 6)-3cos(x+\frac \pi 6)+1=0`,

делаем замену: `cos(x+\frac \pi 6)=y`, тогда `2y^2-3y+1=0`,

находим корни: `y_1=1, y_2=1/2`, откуда следуют два случая:

1. `cos(x+\frac \pi 6)=1`, `x+\frac \pi 6=2\pi n`, `x_1=-\frac \pi 6+2\pi n`.

2. `cos(x+\frac \pi 6)=1/2`, `x+\frac \pi 6=\pm arccos 1/2+2\pi n`, `x_2=\pm \frac \pi 3-\frac \pi 6+2\pi n`.

Ответ: `x_1=-\frac \pi 6+2\pi n`, `x_2=\pm \frac \pi 3-\frac \pi 6+2\pi n`.

Разложение на множители.

Пример. Решить уравнение: `sin x+cos x=1`.

Решение. Перенесем влево все члены равенства: `sin x+cos x-1=0`. Используя , преобразуем и разложим на множители левую часть:

`sin x — 2sin^2 x/2=0`,

`2sin x/2 cos x/2-2sin^2 x/2=0`,

`2sin x/2 (cos x/2-sin x/2)=0`,

1. `sin x/2 =0`, `x/2 =\pi n`, `x_1=2\pi n`.
2. `cos x/2-sin x/2=0`, `tg x/2=1`, `x/2=arctg 1+ \pi n`, `x/2=\pi/4+ \pi n`, `x_2=\pi/2+ 2\pi n`.

Ответ: `x_1=2\pi n`, `x_2=\pi/2+ 2\pi n`.

Приведение к однородному уравнению

Вначале нужно данное тригонометрическое уравнение привести к одному из двух видов:

`a sin x+b cos x=0` (однородное уравнение первой степени) или `a sin^2 x + b sin x cos x +c cos^2 x=0` (однородное уравнение второй степени).

Потом разделить обе части на `cos x \ne 0` — для первого случая, и на `cos^2 x \ne 0` — для второго. Получим уравнения относительно `tg x`: `a tg x+b=0` и `a tg^2 x + b tg x +c =0`, которые нужно решить известными способами.

Пример. Решить уравнение: `2 sin^2 x+sin x cos x — cos^2 x=1`.

Решение. Запишем правую часть, как `1=sin^2 x+cos^2 x`:

`2 sin^2 x+sin x cos x — cos^2 x=` `sin^2 x+cos^2 x`,

`2 sin^2 x+sin x cos x — cos^2 x -` ` sin^2 x — cos^2 x=0`

`sin^2 x+sin x cos x — 2 cos^2 x=0`.

Это однородное тригонометрическое уравнение второй степени, разделим его левую и правую части на `cos^2 x \ne 0`, получим:

`\frac {sin^2 x}{cos^2 x}+\frac{sin x cos x}{cos^2 x} — \frac{2 cos^2 x}{cos^2 x}=0`

`tg^2 x+tg x — 2=0`. Введем замену `tg x=t`, в результате `t^2 + t — 2=0`. Корни этого уравнения: `t_1=-2` и `t_2=1`. Тогда:

1. `tg x=-2`, `x_1=arctg (-2)+\pi n`, `n \in Z`
2. `tg x=1`, `x=arctg 1+\pi n`, `x_2=\pi/4+\pi n`, ` n \in Z`.

Ответ. `x_1=arctg (-2)+\pi n`, `n \in Z`, `x_2=\pi/4+\pi n`, `n \in Z`.

Переход к половинному углу

Пример. Решить уравнение: `11 sin x — 2 cos x = 10`.

Решение. Применим формулы двойного угла, в результате: `22 sin (x/2) cos (x/2) -` `2 cos^2 x/2 + 2 sin^2 x/2=` `10 sin^2 x/2+10 cos^2 x/2`

`4 tg^2 x/2 — 11 tg x/2 +6=0`

Применив описанный выше алгебраический метод, получим:

1. `tg x/2=2`, `x_1=2 arctg 2+2\pi n`, `n \in Z`,
2. `tg x/2=3/4`, `x_2=arctg 3/4+2\pi n`, `n \in Z`.

Ответ. `x_1=2 arctg 2+2\pi n, n \in Z`, `x_2=arctg 3/4+2\pi n`, `n \in Z`.

Введение вспомогательного угла

В тригонометрическом уравнении `a sin x + b cos x =c`, где a,b,c — коэффициенты, а x — переменная, разделим обе части на `sqrt {a^2+b^2}`:

`\frac a{sqrt {a^2+b^2}} sin x +` `\frac b{sqrt {a^2+b^2}} cos x =` `\frac c{sqrt {a^2+b^2}}`.

Коэффициенты в левой части имеют свойства синуса и косинуса, а именно сумма их квадратов равна 1 и их модули не больше 1. Обозначим их следующим образом: `\frac a{sqrt {a^2+b^2}}=cos \varphi`, ` \frac b{sqrt {a^2+b^2}} =sin \varphi`, `\frac c{sqrt {a^2+b^2}}=C`, тогда:

`cos \varphi sin x + sin \varphi cos x =C`.

Подробнее рассмотрим на следующем примере:

Пример. Решить уравнение: `3 sin x+4 cos x=2`.

Решение. Разделим обе части равенства на `sqrt {3^2+4^2}`, получим:

`\frac {3 sin x} {sqrt {3^2+4^2}}+` `\frac{4 cos x}{sqrt {3^2+4^2}}=` `\frac 2{sqrt {3^2+4^2}}`

`3/5 sin x+4/5 cos x=2/5`.

Обозначим `3/5 = cos \varphi` , `4/5=sin \varphi`. Так как `sin \varphi>0`, `cos \varphi>0`, то в качестве вспомогательного угла возьмем `\varphi=arcsin 4/5`. Тогда наше равенство запишем в виде:

`cos \varphi sin x+sin \varphi cos x=2/5`

Применив формулу суммы углов для синуса, запишем наше равенство в следующем виде:

`sin (x+\varphi)=2/5`,

`x+\varphi=(-1)^n arcsin 2/5+ \pi n`, `n \in Z`,

`x=(-1)^n arcsin 2/5-` `arcsin 4/5+ \pi n`, `n \in Z`.

Ответ. `x=(-1)^n arcsin 2/5-` `arcsin 4/5+ \pi n`, `n \in Z`.

Дробно-рациональные тригонометрические уравнения

Это равенства с дробями, в числителях и знаменателях которых есть тригонометрические функции.

Пример. Решить уравнение. `\frac {sin x}{1+cos x}=1-cos x`.

Решение. Умножим и разделим правую часть равенства на `(1+cos x)`. В результате получим:

`\frac {sin x}{1+cos x}=` `\frac {(1-cos x)(1+cos x)}{1+cos x}`

`\frac {sin x}{1+cos x}=` `\frac {1-cos^2 x}{1+cos x}`

`\frac {sin x}{1+cos x}=` `\frac {sin^2 x}{1+cos x}`

`\frac {sin x}{1+cos x}-` `\frac {sin^2 x}{1+cos x}=0`

`\frac {sin x-sin^2 x}{1+cos x}=0`

Учитывая, что знаменатель равным быть нулю не может, получим `1+cos x \ne 0`, `cos x \ne -1`, ` x \ne \pi+2\pi n, n \in Z`.

Приравняем к нулю числитель дроби: `sin x-sin^2 x=0`, `sin x(1-sin x)=0`. Тогда `sin x=0` или `1-sin x=0`.

1. `sin x=0`, `x=\pi n`, `n \in Z`
2. `1-sin x=0`, `sin x=-1`, `x=\pi /2+2\pi n, n \in Z`.

Учитывая, что ` x \ne \pi+2\pi n, n \in Z`, решениями будут `x=2\pi n, n \in Z` и `x=\pi /2+2\pi n`, `n \in Z`.

Ответ. `x=2\pi n`, `n \in Z`, `x=\pi /2+2\pi n`, `n \in Z`.

Тригонометрия, и тригонометрические уравнения в частности, применяются почти во всех сферах геометрии, физики, инженерии. Начинается изучение в 10 классе, обязательно присутствуют задания на ЕГЭ, поэтому постарайтесь запомнить все формулы тригонометрических уравнений — они вам точно пригодятся!

Впрочем, даже запоминать их не нужно, главное понять суть, и уметь вывести. Это не так и сложно, как кажется. Убедитесь сами, просмотрев видео.